【プログラミング】モンテカルロシミュレーションで円周率を推定する

科学技術計算ではよくシミュレーションが行われます。
今回は、シミュレーションの基礎的な例として挙げられるモンテカルロシミュレーションについてまとめます。
シミュレーションの意義や実施する感覚をつかむのに良い題材のように思います。

シミュレーションの役割
モンテカルロシミュレーション
円周率についてのモンテカルロ・シミュレーション
python で記述する
推定精度は低い
余談：pythonにおける科学技術計算の注意

価格: 2970 円
楽天で詳細を見る

シミュレーションの役割

シミュレーションの大きな役割としては、現実では再現しにくい状況を作り出して理論が正しいかを検証することにあります。
ちなみにシミュレーターを作ると理論の理解を深めることがかなり深まるのでシミュレーターが作れるかどうかで実力の見極めが出来たりします。

モンテカルロシミュレーション

モンテカルロ・シミュレーションはシンプルな確率モデルを試行回数を重ねることで、結果を推定しようというものになります。
確率モデルというと難しく聞こえますが、たとえば「2つのサイコロを同時に降ったときの期待を求めよ！」という問題を解くときに、実際に「サイコロを2つ作って降ってみよう」の部分が確率モデルに当たります。つまり、「サイコロを2つ作って降ってみよう」というのをプログラムで作って、それを何百回・何千万回と繰り返すことで、答えを得ようと思います。

上記の例は、確率の問題でもよくあるので簡単に7と想像がつきます。実際、モンテカルロ・シミュレーションは理論自体が複雑で数式で表せなかったり、計算時間がかかりすぎて計算できないときに利用します。

ただし、あくまで「推定」なのでどれくらいその結果精度は試行回数にもよります。

円周率についてのモンテカルロ・シミュレーション

今回は、円周率について調べて推定したいと思います。
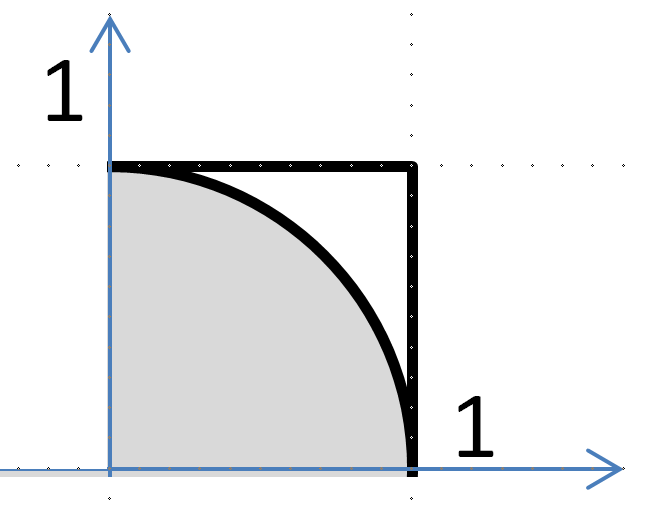
試行する内容は、正方形の範囲にランダムに点を落としてやって、円の部分に落ちた点の数と全体数の比と半月円の面積と正方形の面積の比から推定します。
数式で表すと下式となります。
十分試行回数が大きい場合下式が成り立ちます。

$\displaystyle （円の部分に落ちる点の数）:（全体の点数）＝\frac{ \pi}{4} :1$

円周率について解くと、下式のようになります。

$\displaystyle \pi=\frac{4 (円の部分に落ちた点の数)}{(全体の点数)}$

python で記述する

上の式をpythonで記述すると下のスクリプトのようになります。

# -*- coding: utf-8 -*-

import logging

import numpy as np

logger = logging.getLogger(__name__)

if __name__=="__main__":
    logger.debug("start")
    N_trial=100000000
    n_pi=0
    for i in range(N_trial):
        position_x=np.random.rand()
        position_y=np.random.rand()

        radius=position_x*position_x+position_y*position_y
        if radius<1:
            n_pi=n_pi+1
        else:
            pass

    
    pi_estimate=4*n_pi/N_trial
    print(pi_estimate)

推定精度は低い

計算精度は試行回数に依存します。
理論上、無限の容量のメモリとどんな計算でも一瞬で完了するCPUがあれば計算精度はいくらでも高めることができますが、そんなものは当然ありません。
試しに、1億回計算させてみた結果がこちらとなります。

計算結果：3.1415354
円周率の正しい値：3.14159265359

大きくは外れていないものの小数点6桁目で間違ってますね。
1億回試行してこの状況なので、精度を上げるためにはかなりの時間がかかります。
なので、正確性はある程度犠牲にしたあくまで「推定」にすぎないものと捉えていただくのがよいと思います。

余談：pythonにおける科学技術計算の注意

pythonは科学技術計算で使用されることは多いですが、今回のような数値を正しく求めるような用途にはあまり向いていません。
というのも計算精度が保証されておらず、不確かさを含むことになります。
どれだけの計算精度が欲しいかでプログラミング言語を選んだほうが良いと思います。
基本的には、pythonのようなスクリプト言語はC言語のようなコンパイラ言語より計算精度が低いことが多いです。
たとえば、下のpython スクリプトでは、小数点を正しく計算できません。